Despite advancements in research methods and the growth of large international data sharing initiatives,1 our understanding of the biological underpinnings of psychiatric disorders remains limited. An often cited reason for this stagnation is the presence of “heterogeneity,” whether intrinsic to the condition or an artifact of clinical assessment, sampling, experimental protocol, or otherwise. However, for a concept of such longstanding importance to psychiatric research, we have no consistent framework within which to study heterogeneity itself.
In this editorial, we argue that heterogeneity must be understood and communicated in 2 ways. First, we must have a sense of what heterogeneity is as a mathematical and statistical concept. In this respect, we highlight that heterogeneity is generally viewed as a combination of deviance (the degree of differences between elements in a set) and multimodality (the number of clusters in a set or modes in a mixture distribution), both of which can be expressed in a common and easily interpretable set of units known as the “numbers equivalent” or “effective numbers.”2,3 Second, we must understand that the conceptual relevance of heterogeneity is linked to where (in terms of levels of analysis) it is expressed. That is, heterogeneity gains substantial conceptual power only when discussed with specific reference to the space of features being deemed heterogeneous. Here, too, we argue that the units of numbers equivalent can clarify the level at which heterogeneity is being discussed. A central emphasis of this argument, overall, is that understanding heterogeneity requires us to separate our understanding of it as a quantity from the conditions and features that we deem to be heterogeneous, and the causes thereof.
What is heterogeneity?
This section provides a brief overview of the different perspectives with which heterogeneity has been viewed in psychiatric research: deviance and multimodality. We then unify these components under a single set of units, known in ecology, economics and political science as effective numbers or numbers equivalent.2–5
Deviance
Deviance refers to the degree to which elements in a set or sample differ from one another along one or more characteristics. This is most commonly measured using variance and standard deviation,6 although model-based approaches are increasingly popular in the psychiatric literature.7 There are many other deviance-based heterogeneity indices,8 but their use in the psychiatric literature remains limited at present for reasons we explore further in forthcoming work (unpublished observations, 2019).
Perhaps the most familiar measure of heterogeneity in the sciences is simply the variance. Particularly notable are those versions employed in meta-analysis, including the variance of between-study effects in mixed-effects meta-analysis,9 and the I2 statistic (which involves a decomposition of variance into within- and between-study components).10 Logarithmic ratios of variance (and coefficient of variation) and parametric models of variance have been used in the neuroimaging literature to compare structural brain heterogeneity of patients with schizophrenia against controls.11,12 Taking variance as one’s heterogeneity index assumes that (squared) Euclidean distance of observations from their sample mean is the proper measure of variability in that given system. Unfortunately, this assumption may be overly simplistic when it comes to complex, real-world data.13
Recently, researchers in psychiatric neuroimaging have developed an increasingly popular method, known as “normative modelling,” for characterizing heterogeneity in clinical cohorts.7 This approach begins by using a probabilistic model to learn a distribution of “normal” variation of some clinical or biological feature given some relevant covariate(s), such as age or neuropsychological function. Using extreme value statistics, one then evaluates the degree to which individual participants in some cohort deviate from their predicted normative distribution, assuming that psychiatric disorders will tend to cause stronger deviations from normative ranges over relevant variables. However, although this method can be useful for characterizing sources of heterogeneity, it does not truly measure the amount of heterogeneity in a system.
Multimodality
Multimodality refers to different categories, strata, or distributions being represented within a given set or sample. In the psychiatric literature, the multimodality view of heterogeneity is implied in studies of symptom combination diversity,14 microbial biodiversity15 and diversity of prescribing habits,16,17 to name a few. However, it is the large number of clustering and latent class analyses that signify our field’s tendency to view heterogeneity as reflective of multimodality in our data.
The nature of clinical psychiatric nosology as a set of symptom checklists has prompted many authors to combinatorially enumerate the number of possible symptom groupings for different conditions. In these studies, each symptom combination is a categorical “mode” in the set of all presentations for a given condition. For example, the number of symptom combinations for major depressive disorder in the Diagnostic and Statistical Manual of Mental Disorders, 5th edition,18 can be shown to equal 227,19,20 whereas generalized anxiety disorder (GAD) and borderline personality disorder (BPD) can be shown to have upper bounds of 42 and 256 combinations, respectively.14 Under this perspective, a condition’s heterogeneity is related to the size of the space of all possible clinical presentations. In real-world practice, however, there is substantial inequality in the distribution of symptom combination incidence. Consider that if each of the 42 presentations of GAD were equally likely, but 99.999% of patients with BPD fulfilled all 9 criteria, then BPD would be effectively less heterogeneous than GAD, despite having a larger absolute “space of presentations.”
To address the insensitivity of simple combinatorial enumeration to inequality in the probability of different events, several indices view heterogeneity as a combination of both 1) size of the event space and 2) the level of inequality in the probabilities of those events. These indices do not measure heterogeneity directly, but rather properties that are correlated with heterogeneity. For instance, one may measure the degree of uncertainty in the process of sampling from a population (this index is the Shannon entropy).21 The contents of samples from a more heterogeneous system should be more uncertain. Heterogeneous sets should also be associated with a lower probability of sampling identical pairs and a greater expected absolute difference (with respect to some normalized feature variables). These 2 properties of heterogeneity are captured by the famous Gini index.22 Both the Shannon and Gini indices, or variations thereof, have been used to quantify diversity in psychiatric symptom presentations14 and gut microbial flora15 in psychiatric disorders as well as heterogeneity of psychotropic prescribing patterns.16,17 However, these indices can be difficult to interpret and synthesize because they do not measure heterogeneity directly, but rather common secondary properties of heterogeneous sets.23
Perhaps the most common approach for characterizing heterogeneity in the psychiatric literature has been to count the number of latent clusters or factors inferred from data under some unsupervised learning model. A comprehensive review of these studies is beyond our scope, but many of them have been reviewed elsewhere.24,25 The central point to appreciate is that these studies all implicitly prioritize multimodality over deviance as the sine qua non of heterogeneity. When we measure heterogeneity by latent cluster counting, we are not interested in the absolute amount of deviation between observations, but rather only in the aggregation of samples into effectively homogeneous groups. Once the individuals are aggregated into defined clusters, they are treated as now belonging to categorical groups between which deviance is maximal and symmetric, and within which deviance is absent, since observations are now treated categorically.
Unfortunately, cluster counting approaches have several problems. Perhaps the most significant is related to cluster validity, reproducibility, and the appropriateness of one clustering approach compared with another.24 Second, since latent classes are viewed as categorical, these methods ignore any within- and between-cluster heterogeneity after the classes have been inferred; for instance, there would be no accounting for the fact that apples are more similar to pears than they are to asphalt. Finally, and perhaps most straightforward, is that the absolute number of clusters will encounter similar problems as the combinatorial symptom enumeration methods discussed above, wherein inequality in cluster sizes is not accounted for in the reported “amount” of heterogeneity.
The effective numbers (or numbers equivalent)
Deviance and multimodality are distinct insofar as they evince one’s assumptions about the “smoothness” of differences between observations in a sample. In situations where the phenomenon of interest is thought to be a spectrum, then heterogeneity is typically formalized and communicated in terms that emphasize relative “distances” between subjects. However, when the phenomenon of interest is thought to have an internal stratification, the multimodality view is dominant. The normative modelling paradigm takes a combined perspective where extreme value testing can be used to identify “deviant modes.” Yet, these perspectives all manifest in the same practical conclusion: heterogeneous systems all generate a larger number of unique observations.
If a system generates a larger number of observations, then it must have an effectively larger event space. This will be the case regardless of whether one is considering heterogeneity as deviance or multimodality. The word “effective” here is critical, because it accounts for the fact that some systems with large potential event spaces may be “effectively” small if most of the sampling probability is attached to only a few events (as in our earlier example comparing GAD and BPD).
Through an index known as Rényi heterogeneity (synonymous with the Hill numbers26 in ecology or the Hannah–Kay27 index in economics), we can in fact measure a system’s heterogeneity in units of numbers equivalent. The Rényi heterogeneity is defined as
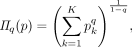 (1)
(1)where q ≥ is a parameter that governs sensitivity to rare events. As a simple example, consider a patient with bipolar disorder who spends 90% of his time depressed, 8% of his time manic and 2% of his time euthymic. Plugging the distribution into the equation above gives
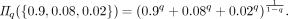
At q = 0 the relative probabilities are ignored, and we obtain the patient’s effective number of total mood states (Π0 = 3). At the limit of q → 1, we obtain the patient’s effective number of typical mood states (Π1 = 1.5), and at q = 2 we obtain the patient’s effective number of common mood states (Π2 = 1.2). Given a set of mood state labels for the same patient within 2 or more time windows, significance of differences in mood-state heterogeneity may be computed most flexibly by comparison of bootstrap estimated confidence intervals of the Rényi heterogeneity in those 2 states. In the specific case of affective time-series data, for example, such statistical procedures may enable a more precise quantification of the “evolution” of heterogeneity of mood states within and between individuals.
Note that as we increase q, the measure becomes progressively less sensitive to the presence of the less common states. When we cannot be assured that our sample covers the whole event space — that is, when a system of interest is thought to have a large event space populated mainly by many very rare events (such as the set of species in a gut microbiome) — the value of q is generally set higher (typically q ≥ 2 ). We recommend a default setting of q = 1, which proportionally weights common and rare classes and corresponds to the commonly used perplexity measure.
Although the resolution parameter q introduces some nuances that are beyond our current scope, the central feature of this measure can be observed nonetheless. Specifically, its results are always reported in terms of the size of the event space. This has 3 benefits. First, it is easily understood since it relies only on the intuitive concepts of counts and sizes. Second, it respects a scaling law known as “the replication principle,”23 which means that doubling the effective number of observations will result in a doubling of the Rényi heterogeneity. Conversely, other indices such as the Shannon entropy, Gini index, and variance will respond idiosyncratically to changes in the size of the event space, and none will respect this doubling property.
The final benefit of measuring heterogeneity in terms of event space size is that it forces us to clearly specify the characteristics and event space of the system whose heterogeneity is being measured. For instance, we defined the affective event space as {Depressed, Manic, Euthymic} in the example above. Readers who astutely identified that the heterogeneity value reported could be invalidated by the overly simplistic 3-category “affective event space,” have (perhaps implicitly) exploited this very benefit of Rényi heterogeneity. Under our formulation, it is insufficient to simply refer to a disorder as “clinically heterogeneous,” “genetically heterogeneous,” or worse still, “heterogeneous” in a more general sense. Where one given disorder may be thought of as heterogeneous because of a large effective number of presentations, another may be considered heterogeneous by virtue of a large effective number of causal genetic variants. To this end, we bring further attention to the “localization” of heterogeneity measurement at different levels of analysis.
Where is the heterogeneity?
If we are to report heterogeneity in terms of an effective number, we must clearly answer the question: effective numbers of what? This question is nontrivial, since the heterogeneity of psychiatric (and other) disorders may differ in degree and relevance across levels of analysis (e.g., genetic, structural, physiologic, symptomatic, or otherwise). For instance, syphilis is counted among one of medicine’s “great imitators” chiefly because of its large number of clinical presentations. However, it is etiologically homogeneous, with all cases caused by the spirochete, Treponema pallidum. Therefore, conditions such as syphilis may be understood as entailing a sort of “distal expansion” of heterogeneity, with the point of expansion beginning at the infection.
In relation to syphilis, other conditions such as, for instance, amyotrophic lateral sclerosis (ALS), might be thought to entail a “contraction” in heterogeneity across levels of analysis (i.e across genetic → molecular → cellular → ......... → clinical levels). Historically, this condition has been sufficiently homogeneous from clinical and electrophysiological perspectives to be distinct from other motor neuron diseases, but it has substantial underlying genetic diversity. There are at least 20 autosomal dominant genetic causes alone of familial ALS, the most prominent of which may be those involving the superoxide dis-mutase gene (SOD1), itself a family of at least 6 mutations (A4V missense, I113T, A4T, H46R, A89V, G93C).28
The metaphor of a condition such as ALS representing a “contraction” of heterogeneity from etiology to clinical presentation may seem clear only in relation to a clear “expansion” associated with syphilis infection. However, identifying relative differences in heterogeneity across levels of analysis is not straightforward, since one may always identify novel but insignificant variations in genetic makeup, biological structure, or clinical presentation. This problem provides still further motivation for emphasizing the feature space upon which heterogeneity is being reported, because comparing effective numbers of 10 and 20 genetic variants is certainly more meaningful than comparing an effective number of 10 genetic variants to 5 clinical phenotypes.
An additional point at which heterogeneity measurement may be relevant is with respect to factors outside of the patient entirely, instead being associated with diagnostic instruments, clinical practices, treatment protocols and research methods. Quantifying heterogeneity at these levels is an important step toward better isolating and measuring heterogeneity of psychiatric disorders.
Conclusion
Heterogeneity is the degree to which a system diverges from a state of perfect internal similarity. Many psychiatric studies have attempted to describe heterogeneity of clinical cohorts by either quantifying some form of deviance or multimodality in their data. However, we have yet to develop a consistent operational framework within which to measure and communicate heterogeneity. Developing such a framework will first require (A) adopting a common set of easily understandable units for heterogeneity measures, and (B) clarifying the different levels of analysis at which heterogeneity manifests.
Adopting measures with units of numbers equivalent is an important first step to advance the precision with which we can study heterogeneity in psychiatric research. These measures are well developed and accepted particularly in ecological applications,23 but we must further evaluate their strengths and limitations for psychiatric research applications. One particular limitation that must be confronted is the fact that numbers equivalent heterogeneity measures currently require the system’s event space to have a categorical component. As it stands, this will be problematic in scenarios where the categorical groupings of patients are either unreliable or of questionable validity.
The formulation of Rényi heterogeneity makes it clear that the “causes” of heterogeneity will depend on the system whose heterogeneity is being measured. For instance, the effective number of clinical presentations of major depressive disorder will depend on one’s diagnostic criteria. Alternatively, the effective number of neurostructural phenotypes in bipolar disorder may be influenced by pharmacological treatments and diversity thereof. The Rényi measure will fortunately admit a statistical procedure for identifying causes or correlates of heterogeneity. In the latter example, if one can model a probability distribution over the space of structural brain images (which can be done using standard unsupervised learning methods), then the effects of medication use on neurostructural heterogeneity can be isolated by exploiting a decomposition of the Rényi heterogeneity (originally proven by the ecologist Lou Jost),29 whose technical details we expand upon in an upcoming review for psychiatric research audiences (unpublished observations, 2019). Such a procedure for isolating heterogeneity caused by exogenous factors may better enable us to characterize the heterogeneity intrinsic to the primary system of interest; the ability to precisely quantify and decompose heterogeneity using the Rényi measure is a step in this direction.
The greater precision afforded by developing rigorous measures of heterogeneity will undoubtedly require us to speak of the heterogeneity of conditions in terms of more specific levels of analysis. This will likely bring about another challenge: measuring only heterogeneity that is relevant to the phenomenon in question. For example, 2 brain images of the same person may deviate from each other based on scanner noise, yet the semantic content of those images — which may be known a priori or identifiable only by unsupervised feature learning models such as autoencoders — is homogeneous. The specificity enforced by reporting heterogeneity as “the effective number of X” could serve as such a filter, since presumably one must justify why the heterogeneity of X is sufficiently important to measure its numbers equivalent. However, answers to these questions await the results of real-world applications of these measures to psychiatric research problems.
Footnotes
The views expressed in this editorial are those of the author(s) and do not necessarily reflect the position of the Canadian Medical Association or its subsidiaries, the journal’s editorial board or the Canadian College of Neuropsychopharmacology.
Competing interests: None declared.
Funding: The authors receive funding from Genome Canada (A. Nunes, M. Alda); the Dalhousie Department of Psychiatry Research Fund (A. Nunes, M. Alda); the Canadian Institutes of Health Research grant #64410 (M. Alda); a Nova Scotia Health Research Foundation Scotia Scholars Graduate Scholarship (A. Nunes); and a Killam Postgraduate Scholarship (A. Nunes).